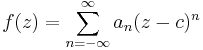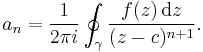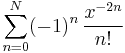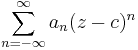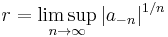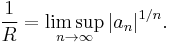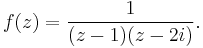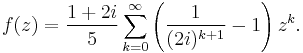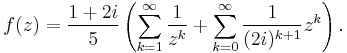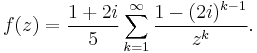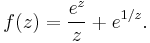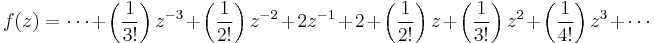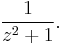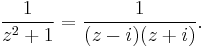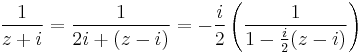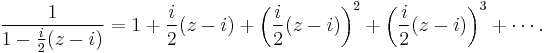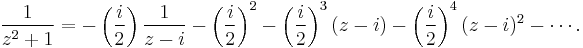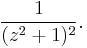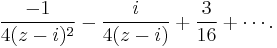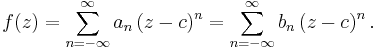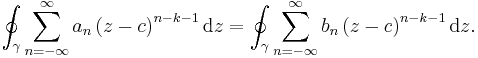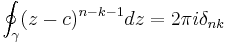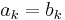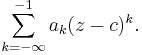Laurent series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in 1841 but did not publish it at the time.
The Laurent series for a complex function f(z) about a point c is given by:
where the an are constants, defined by a line integral which is a generalization of Cauchy's integral formula:
The path of integration γ is counterclockwise around a closed, rectifiable path containing no self-intersections, enclosing c and lying in an annulus A in which 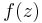 is holomorphic (analytic). The expansion for
is holomorphic (analytic). The expansion for 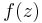 will then be valid anywhere inside the annulus. The annulus is shown in red in the diagram on the right, along with an example of a suitable path of integration labeled
will then be valid anywhere inside the annulus. The annulus is shown in red in the diagram on the right, along with an example of a suitable path of integration labeled  . If we take
. If we take  to be a circle
to be a circle 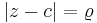 , where
, where 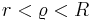 , this just amounts to computing the complex Fourier coefficients of the restriction of
, this just amounts to computing the complex Fourier coefficients of the restriction of  to
to  . The fact that these integrals are unchanged by a deformation of the contour
. The fact that these integrals are unchanged by a deformation of the contour  is an immediate consequence of Stokes' theorem.
is an immediate consequence of Stokes' theorem.
In practice, the above integral formula may not offer the most practical method for computing the coefficients 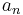 for a given function
for a given function 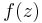 ; instead, one often pieces together the Laurent series by combining known Taylor expansions. Because the Laurent expansion of a function is unique whenever it exists, any expression of this form that actually equals the given function
; instead, one often pieces together the Laurent series by combining known Taylor expansions. Because the Laurent expansion of a function is unique whenever it exists, any expression of this form that actually equals the given function 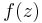 in some annulus must actually be the Laurent expansion of
in some annulus must actually be the Laurent expansion of 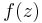 .
.
Contents |
Convergent Laurent series
Laurent series with complex coefficients are an important tool in complex analysis, especially to investigate the behavior of functions near singularities.
Consider for instance the function 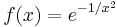 with
with 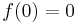 . As a real function, it is infinitely often differentiable everywhere; as a complex function however it is not differentiable at x = 0. By replacing x by −1/x2 in the power series for the exponential function, we obtain its Laurent series which converges and is equal to ƒ(x) for all complex numbers x except at the singularity x = 0. The graph opposite shows e−1/x2 in black and its Laurent approximations
. As a real function, it is infinitely often differentiable everywhere; as a complex function however it is not differentiable at x = 0. By replacing x by −1/x2 in the power series for the exponential function, we obtain its Laurent series which converges and is equal to ƒ(x) for all complex numbers x except at the singularity x = 0. The graph opposite shows e−1/x2 in black and its Laurent approximations
for N = 1, 2, 3, 4, 5, 6, 7 and 50. As N → ∞, the approximation becomes exact for all (complex) numbers x except at the singularity x = 0.
More generally, Laurent series can be used to express holomorphic functions defined on an annulus, much as power series are used to express holomorphic functions defined on a disc.
Suppose
is a given Laurent series with complex coefficients an and a complex center c. Then there exists a unique inner radius r and outer radius R such that:
- The Laurent series converges on the open annulus A := {z : r < |z − c| < R}. To say that the Laurent series converges, we mean that both the positive degree power series and the negative degree power series converge. Furthermore, this convergence will be uniform on compact sets. Finally, the convergent series defines a holomorphic function ƒ(z) on the open annulus.
- Outside the annulus, the Laurent series diverges. That is, at each point of the exterior of A, the positive degree power series or the negative degree power series diverges.
- On the boundary of the annulus, one cannot make a general statement, except to say that there is at least one point on the inner boundary and one point on the outer boundary such that ƒ(z) cannot be holomorphically continued to those points.
It is possible that r may be zero or R may be infinite; at the other extreme, it's not necessarily true that r is less than R. These radii can be computed as follows:
We take R to be infinite when this latter lim sup is zero.
Conversely, if we start with an annulus of the form A = {z : r < |z − c| < R} and a holomorphic function ƒ(z) defined on A, then there always exists a unique Laurent series with center c which converges (at least) on A and represents the function ƒ(z).
As an example, let
This function has singularities at z = 1 and z = 2i, where the denominator of the expression is zero and the expression is therefore undefined. A Taylor series about z = 0 (which yields a power series) will only converge in a disc of radius 1, since it "hits" the singularity at 1.
However, there are three possible Laurent expansions about z = 0, depending on the region z is in:
- One is defined on the disc where |z| < 1; it is the same as the Taylor series,
(The technique involves using partial fractions to split the original expression for f(z) into two simpler fractions and then exploiting the fact that 1/(1-z) is the formula for the sum of a geometric series with first term 1 and constant multiplier z.)
- Another one is defined on the annulus where 1 < |z| < 2, caught between the two singularities,
- The third one is defined on the infinite annulus where 2 < |z| < ∞,
-
- (The terms above can be derived through polynomial long division or using the sum of a geometric series trick again, this time using
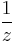 and
and 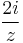 as the common ratios.)
as the common ratios.)
The case r = 0, i.e. a holomorphic function ƒ(z) which may be undefined at a single point c, is especially important.
The coefficient a−1 of the Laurent expansion of such a function is called the residue of ƒ(z) at the singularity c; it plays a prominent role in the residue theorem.
For an example of this, consider
This function is holomorphic everywhere except at z = 0. To determine the Laurent expansion about c = 0, we use our knowledge of the Taylor series of the exponential function:
and we find that the residue is 2.
Example
Find the Laurent series in powers of z − i of
First note that
Now,
The latter fraction can be expanded in a geometric series for z close to i:
We need to multiply the series by the former fraction, −i/2. If we do this and divide both sides by z − i we obtain the following:
As another example, consider finding the Laurent series of the square of the above function,
For this, we can simply square the series that we just derived. Note that for each degree, there are only finitely many terms which multiply together to give that degree. In our example, the degree −2 term of the result is the square of the degree −1 term of the original series, and the degree −1 term is twice the product of the degree −1 and 0 terms. The result is:
Uniqueness
Suppose a function ƒ(z) holomorphic on the annulus r < |z − c| < R has two Laurent series:
Multiply both sides with 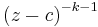 , where k is an arbitrary integer, and integrate on a path γ inside the annulus,
, where k is an arbitrary integer, and integrate on a path γ inside the annulus,
The series converges uniformly on 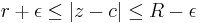 , where ε is a positive number small enough for γ to be contained in the constricted closed annulus, so the integration and summation can be interchanged. Substituting the identity
, where ε is a positive number small enough for γ to be contained in the constricted closed annulus, so the integration and summation can be interchanged. Substituting the identity
into the summation yields
Hence the Laurent series is unique.
Laurent polynomials
A Laurent polynomial is a Laurent series in which only finitely many coefficients are non-zero. Laurent polynomials differ from ordinary polynomials in that they may have terms of negative degree.
Principal part
The principal part of a Laurent series is the series of terms with negative degree , that is
If the principal part of f is a finite sum, then f has a pole at c of order equal to (negative) the degree of the highest term; on the other hand, if f has an essential singularity at c, the principal part is an infinite sum (meaning it has infinitely many non-zero terms).
If the inner radius of convergence of the Laurent series for f is 0, then this is if and only if: f has an essential singularity at c if and only if the principal part is an infinite sum, and has a pole otherwise.
If the inner radius of convergence is positive, f may have infinitely many negative terms but still be regular at c, as in the example above, in which case it is represented by a different Laurent series in a disk about c.
Laurent series with only finitely many negative terms are tame—they are a power series divided by 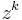 , and can be analyzed similarly—while Laurent series with infinitely many negative terms have complicated behavior on the inner circle of convergence.
, and can be analyzed similarly—while Laurent series with infinitely many negative terms have complicated behavior on the inner circle of convergence.
Multiplication
Laurent series cannot in general be multiplied. Algebraically, the expression for the terms of the product may involve infinite sums which need not converge (one cannot take the convolution of integer sequences). Geometrically, the two Laurent series may have non-overlapping annuli of convergence.
Two Laurent series with only finitely many negative terms can be multiplied: algebraically, the sums are all finite; geometrically, these have poles at c, and inner radius of convergence 0, so they both converge on an overlapping annulus.
Thus when defining formal Laurent series, one requires Laurent series with only finitely many negative terms.
Similarly, the sum of two convergent Laurent series need not converge, though it is always defined formally, but the sum of two bounded below Laurent series (or any Laurent series on a punctured disk) has a non-empty annulus of convergence.
See also
- Formal Laurent series — Laurent series considered formally, with coefficients from an arbitrary commutative ring, without regard for convergence, and with only finitely many negative terms, so that multiplication is always defined.
- Z-transform — the special case where the Laurent series is taken about zero has much use in time series analysis.
- Fourier series — the substitution
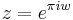 transforms a Laurent series into a Fourier series, or conversely. This is used in the q-series expansion of the j-invariant.
transforms a Laurent series into a Fourier series, or conversely. This is used in the q-series expansion of the j-invariant.